term

definition

another definition

While working on the forthcoming version of my DoubleUSM script, which I’m porting to HTML Panels, I’ve run into the following problem: how do you fit a large range – say, (1..500) with floating point precision – into a Slider which has, at best, less than 200 possible, real slots? Nonlinear sliders and Vue.js Computed Properties are the answer, read along.

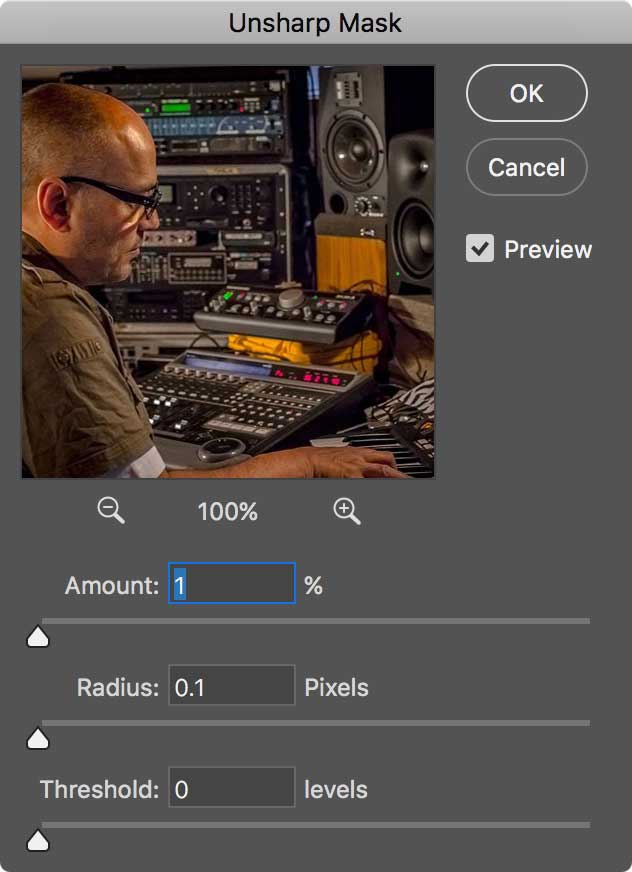
If you play with the Photoshop UnSharp Mask dialog, which looks like what you see here, you’ll notice that the three sliders work in a very different fashion.

And I’m not only talking about the sheer range: Amount is 1..500 (integer), Radius 0.1..1000 (floating point, 10.000 possible values!), Threshold 1..255 (integer).

Perhaps more importantly, the sweetest range of each parameter – i.e. the most probable, or used – is different. As a consequence Adobe engineers have expanded it, to the detriment of other, less probable values. An example: the Radius, in a so-called traditional USM, rarely goes beyond 3px, depending on the image size. Let’s say 5px, or even 10px to be on the ultra-safe side. When it comes to inverse USM (or as my color correction maestro Dan Margulis would call it, HiRaLoAm: High Radius, Low Amount) Radius can go up to 50px, or even more. Not more than 100px, I’d bet, in 98.98% of every HiRaLoAm run in the civilized world. Let’s forget Adobe’s crazy ceiling of 1000px: I’ll stick to a maximum value of 500px. You’re facing a couple of issues:

1. Fitting 5000 values into a Slider that, at best, is 200px wide.
2. Expanding and compressing parts of the [0.1..500] slider span so that the more used/probable ranges have more coverage.

I’m going to use the following very simple setup as a starting point:

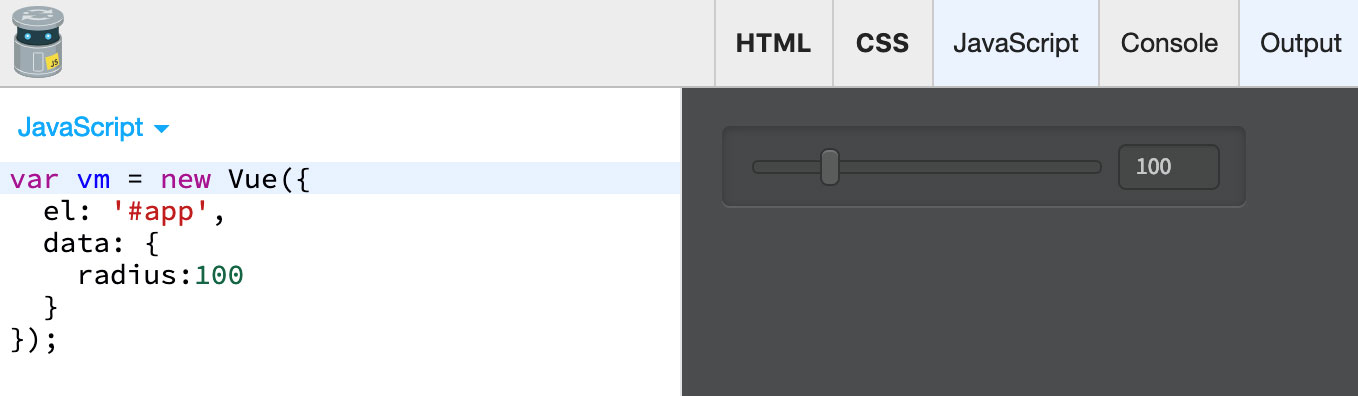
As you see, I’ve bound the slider (aka input of type range, width of 175 pixels) and the number box (input of type number: I’ve hidden the spin boxes because I think they’re ugly) to the same radius property using v-model. It kinda works, but functionally, as a Radius slider, it’s unusable. I can’t precisely target any small value (say 0.4), because the whole slider is just too tiny to keep track of them: the first available value is 2.3! How did Adobe solve that issue? The only way to find it is experimentally: I’ve grabbed screenshots of the USM dialog at different Radius values, and measured the pixel span of the slider thumb aka handler. Annoying, and perhaps not ideal, but it worked. I’ve used a spreadsheet to graph the range pixels span (first column), against the radius value (last column)

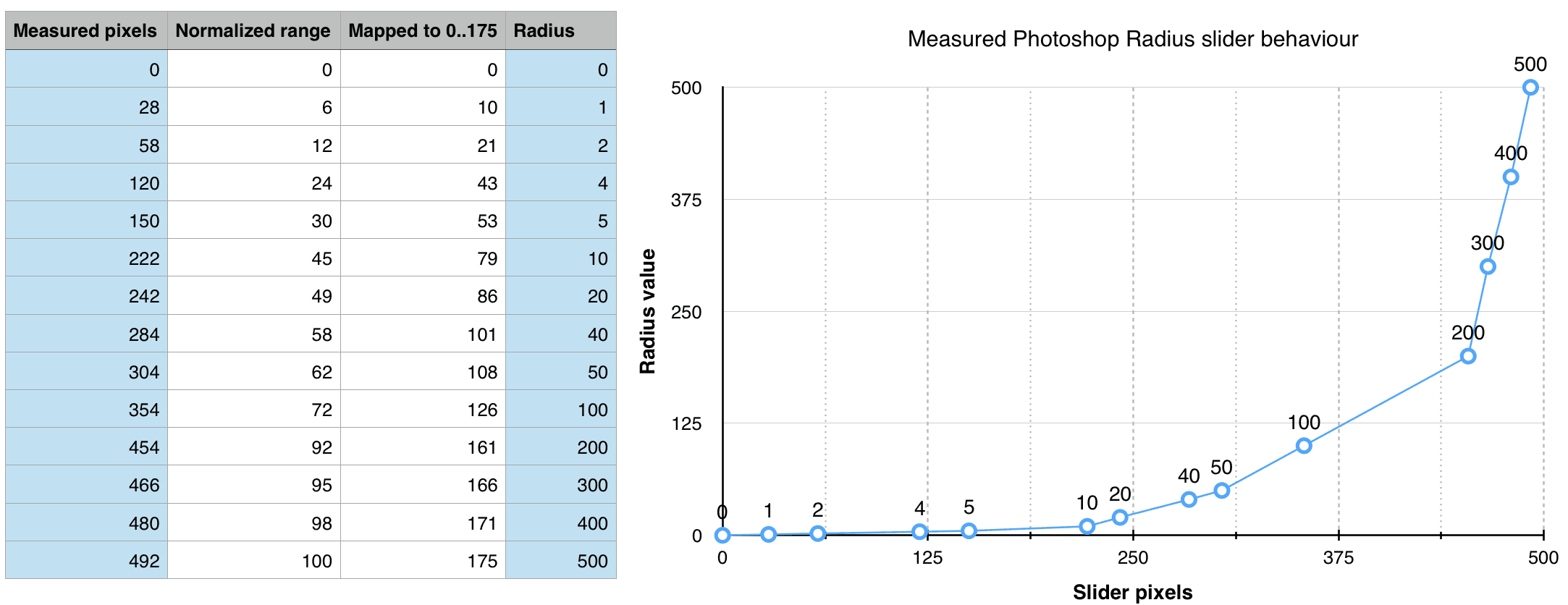
As you see, the original Adobe’s slider spans about 500 actual pixels to cover 500 integer values: problem is that the Radius is expressed as floating point, and the behaviour is highly nonlinear, as the graph shows. Move the handler about halfway through (242px) and the Radius is only 20px (and not 250px), a twenty-fifth of the entire range has been very much expanded. In the spreadsheet I’ve added two column, with normalized values (0..100) of the measured pixels, then mapped to my original slider actual values of the Slider, that will be of some use later on.

You’ll forgive me if I’m a bit imprecise with these calculations. Fact is that I have no idea whether a 175px width slider has room, for its thumb/handler, for 175 actual different positions when you drag it. I’ve set in the HTML its min=0 and max=175, roughly matching its current width in pixels. BTW 0..175 is a range of 176 values.

Looking at the graph, you can see four separate, linear segments: [0..10], [10..50], [50..200], [200..500], which is bearable: this is what they do, and I could perhaps replicate them. I’m afraid it doesn’t suit my own taste so I’ll change the mapping to fit my own idea of the proper slider behaviour for USM Radius. And the way to do that is via VueJS Computed Properties. The idea is that we’ll bind (via v-model) the spinner (number field) to the same radius property of the initial example, while the slider to another prop called  sliderRadius, calculated on the fly from radius. This goes in the computed section of the Vue instance, see below (please note that I’m returning the same, unprocessed value for now).

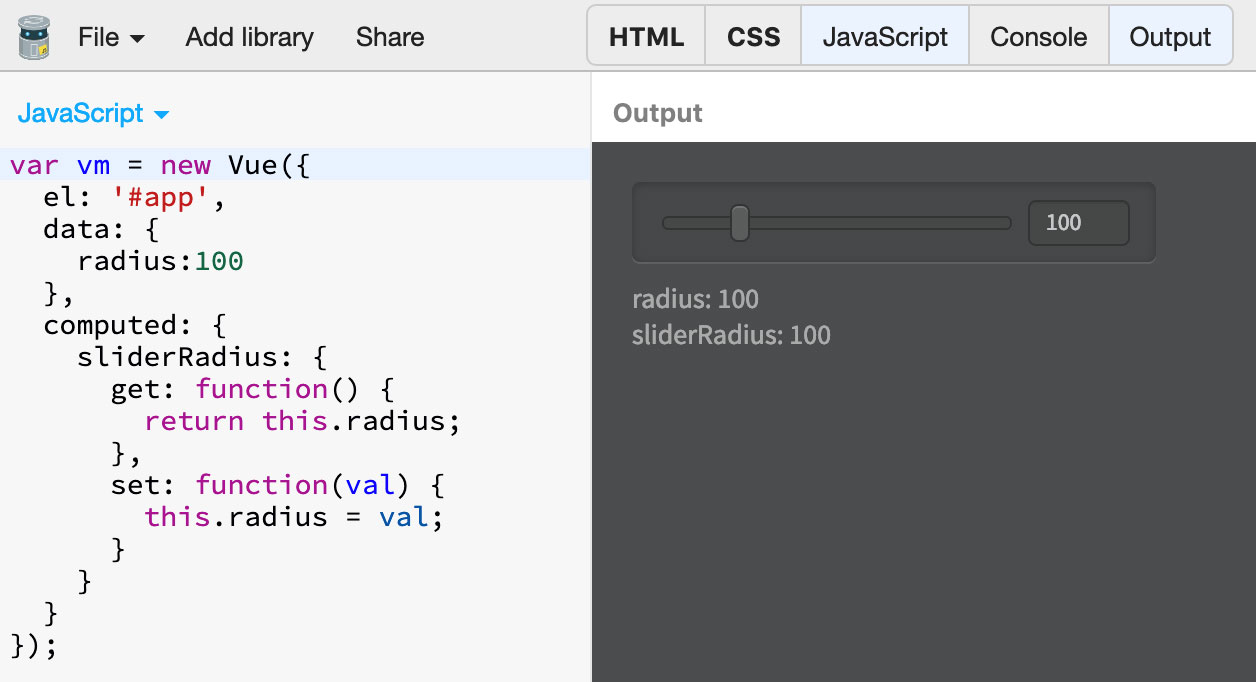
The getter here is the function that computes sliderRadius from radius, while the setter does the reverse (sets the radius from sliderRadius). In practice, the getter is involved when you type number values in the spinner; the setter when you drag the slider. With this in place, it’s time to compute the two functions. I’ve decided that four linear ranges like [0..5], [5..30], [30..100], [100..500] are a better fit for me – see the following graph.

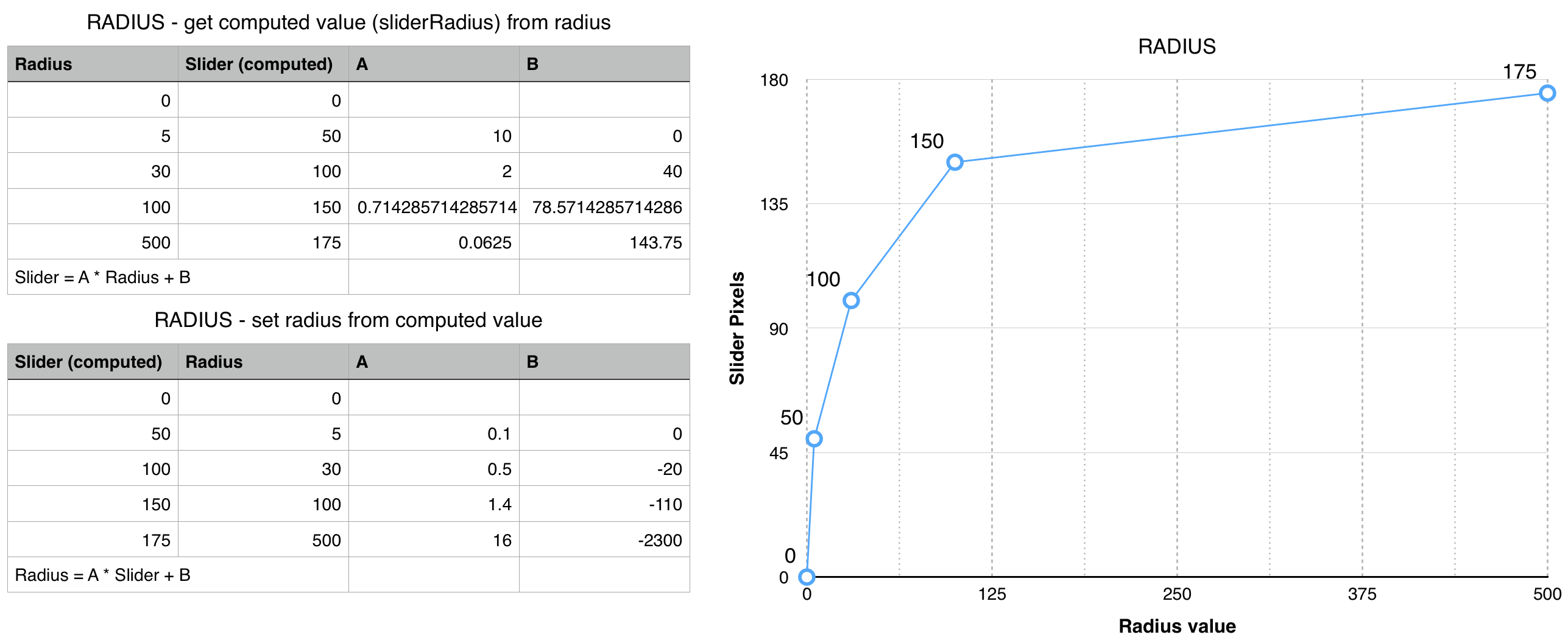
In case you’re dubious, I’m plotting now Radius in the $ x $, Slider in the $ y, $  whereas the in previous graph I did the reverse (Slider $ x $, Radius $ y $). I’ve set the points so that there is a (theoretical) match for the important ranges. For instance, the Radius range [0..5] is mapped to [0..50] in the slider, so that (theoretically) each point value (0, 0.1, 0.2, 0.3…) has a perfect match with the slider (0, 1, 2, 3, and so on). At least this is what I hope is the case, because – as I’ve written – there’s no guarantee that a 175px slider has 175 available positions for the thumb. Now it’s only a matter of finding the $ a $ and $ b $ coefficient for a linear equation $ y = ax + b $. Solving that for $ a, b $ is easy: $ a $ is rise over run e.g. for the getter in the second range [5..30]:

We know all the Radius/Slider pairs, so b is got substituting the x,y and recently found a values in the linear equation, eg.

As a result, the linear equation for the second range [5..30] getter is:

That’s for the getter. You have to invert Slider and Radius to obtain setter coefficients, so for instance (setter, second range):

Which translates into the following code:

var vm = new Vue({
  el: '#app',
  data: {
    radius: 100
  },
  computed: {
    sliderRadius: {
      get: function() {
        var val = this.radius;
        if (val <= 5) {
          return val * 10;
        } else if (val <= 30) {
          return val * 2 + 40;
        } else if (val <= 100) {
          return val * 0.714285714285714 + 78.5714285714286;
        } else {
          return val * 0.0625 + 143.75;
        }
      },
      set: function(val) {
        val = +val;
        if (val <= 50) {
          this.radius = Math.round10(val * 0.1, -1);
        } else if (val <= 100) {
          this.radius = Math.round10(val * 0.5 - 20, -1);
        } else if (val <= 150) {
          this.radius = Math.round10(val * 1.4 - 110, -1);
        } else {
          this.radius = Math.round10(val * 16 - 2300, -1);
        }
      }
    }
  }
});

I’ve added a Math.round10 function borrowed from MDN, which allows me to send to the spinner properly formatted numbers. Also note that I’ve changed accordingly the HTML, limiting the slider to max=175 and, importantly, setting the step to 0.1: otherwise, when you change numbers in the steppers, the slider would jump. The final, working JSBin is this one:

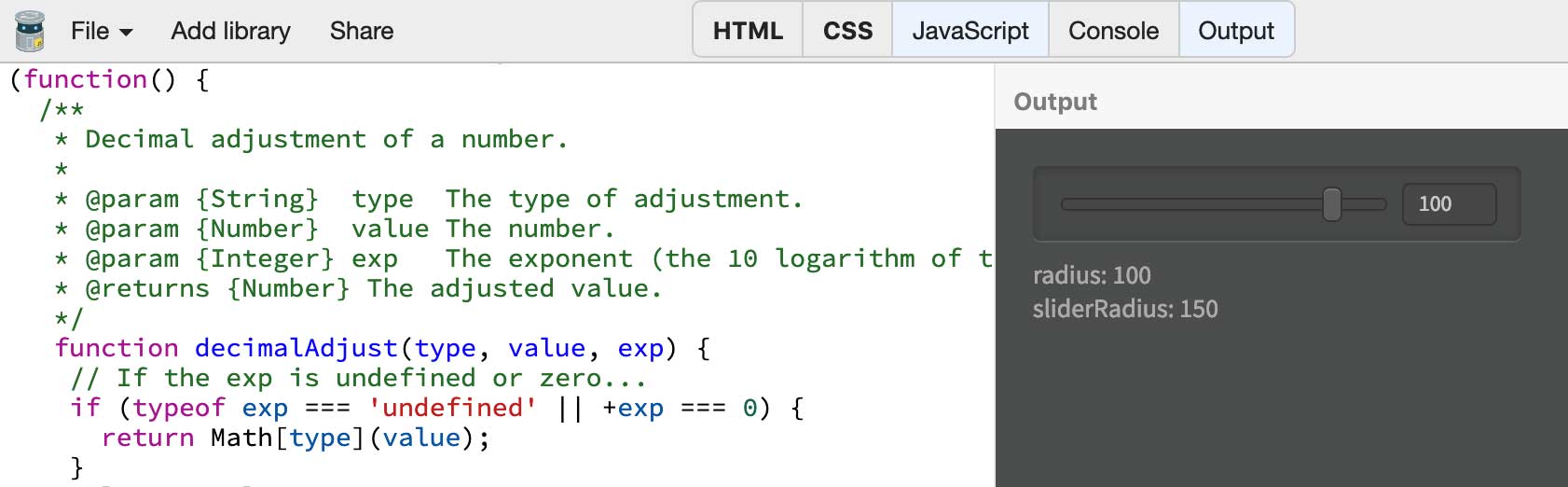
As you see, it maps correctly small floating point values, then ramps up nicely and compresses high, less used Radii. Which doesn’t mean that you can’t set them, because you can always type, say, 489.3px in the spinner, and bind that value to your actual Photoshop JSX function call. It’s not rocket science at all, but it took me some time to put this together for my own panels – that’s why I’m sharing here, both for you and my future, senior self 😉

If you’re into Vue.js, you might want to check also: Vue.js – Binding a Component in a v-for loop to the Parent model.